用函数画画

Posted on 2025-11-01

突然想要整理一下高中时候写的一个有趣的小东西。是有关怎么用函数来画画的。顺便学习下怎么用Markdown来写一些简单的数学公式。

话不多说，我们直接进入正题。

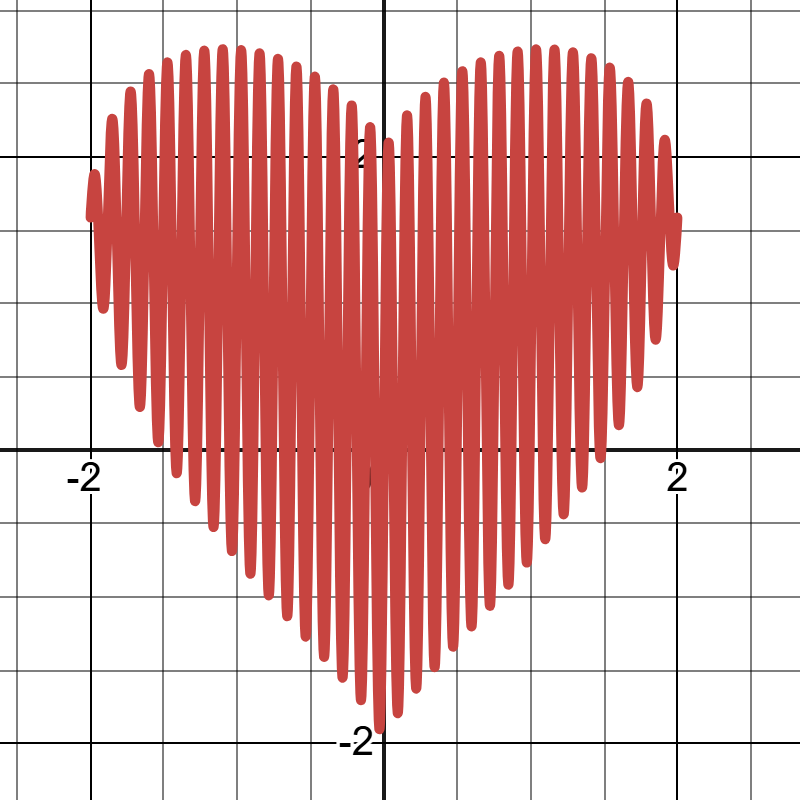
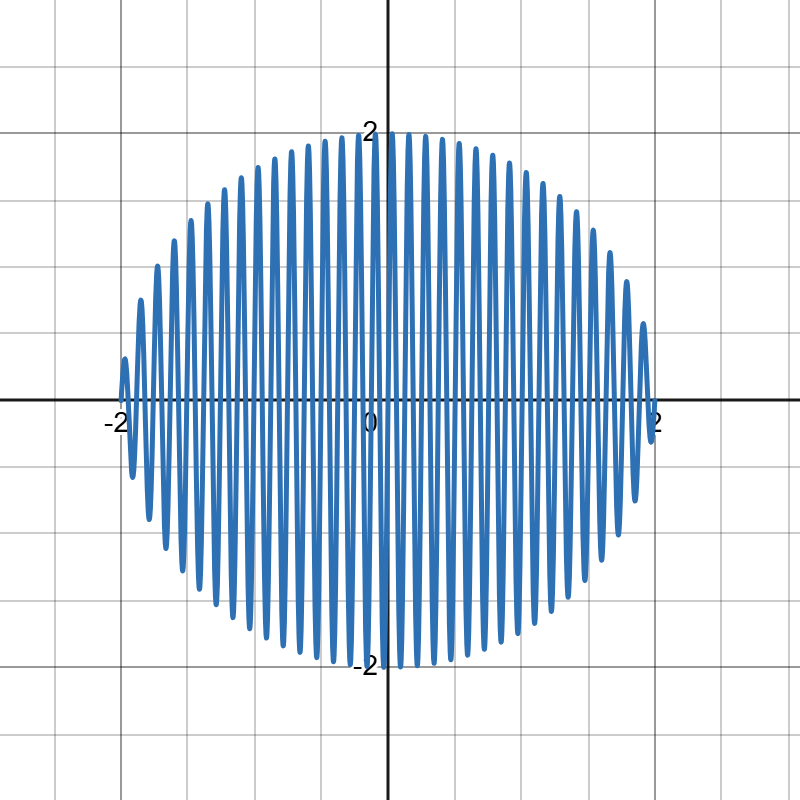
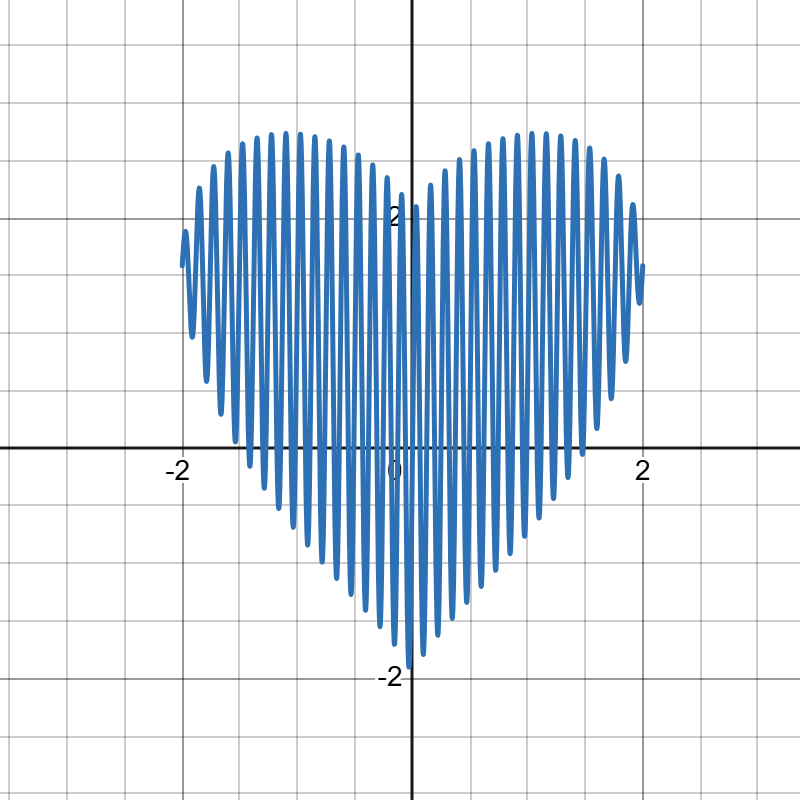
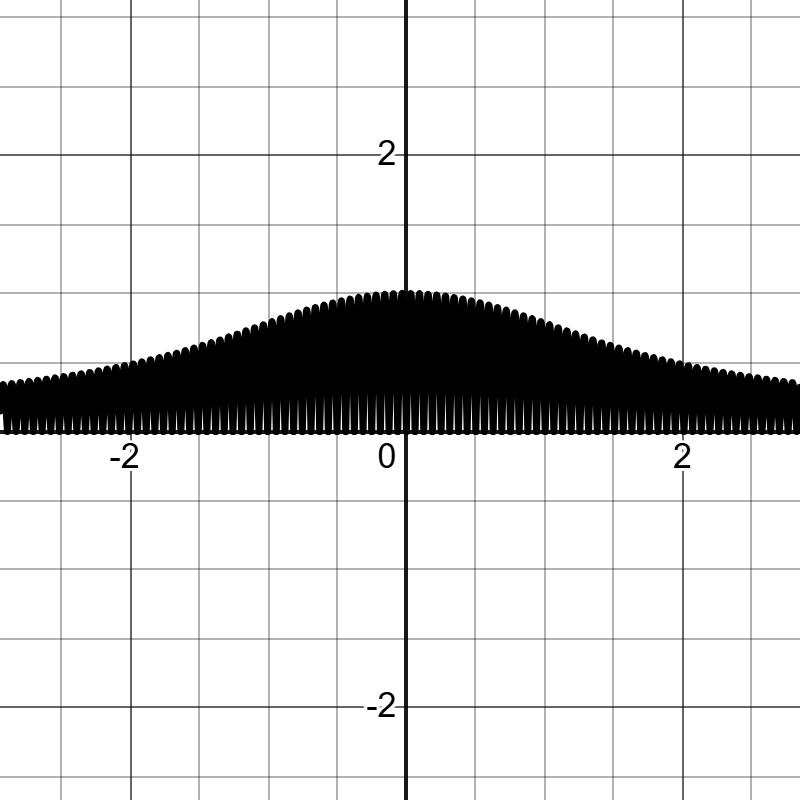
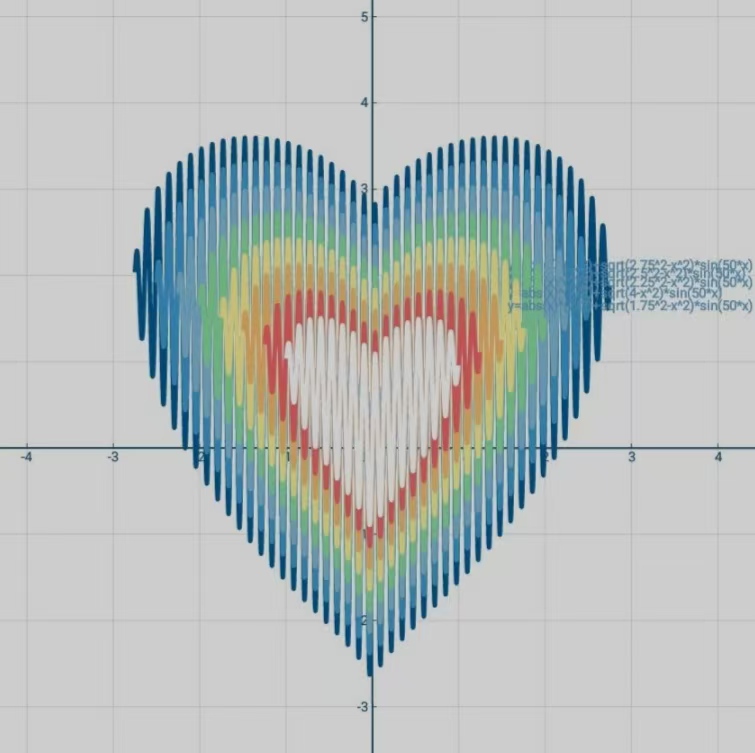
如图1，是一个爱心函数，其解析式为： \[f(x) = \lvert x\rvert ^\frac{2}{3} + \sqrt{4-x^2}\sin{50x}\] 很神奇，对不对？这个式子是怎么得出来的呢？下面先介绍Egger原创的画图函数公式： \[f(x) = [g(x)+h(x)\sin{50x}][(n-x)(x-m)]^\frac{1}{1000}\] 其中\(g(x)\)用于控制函数图像的拉伸变换，\(h(x)\)用于控制函数图像的形状，\(\sin{50x}\)用于控制函数图像的填充，这里的系数50是一个经验值，系数越大填充越密。\([(n-x)(x-m)]^\frac{1}{1000}\)用于控制函数图像的定义域，这里的\(\frac{1}{1000}\)也是一个经验值，可以根据具体情况修改。

那么这个式子是如何得出来的呢。接下来将一一讲述：

一、函数的填充：\(h(x)\sin{50x}\)

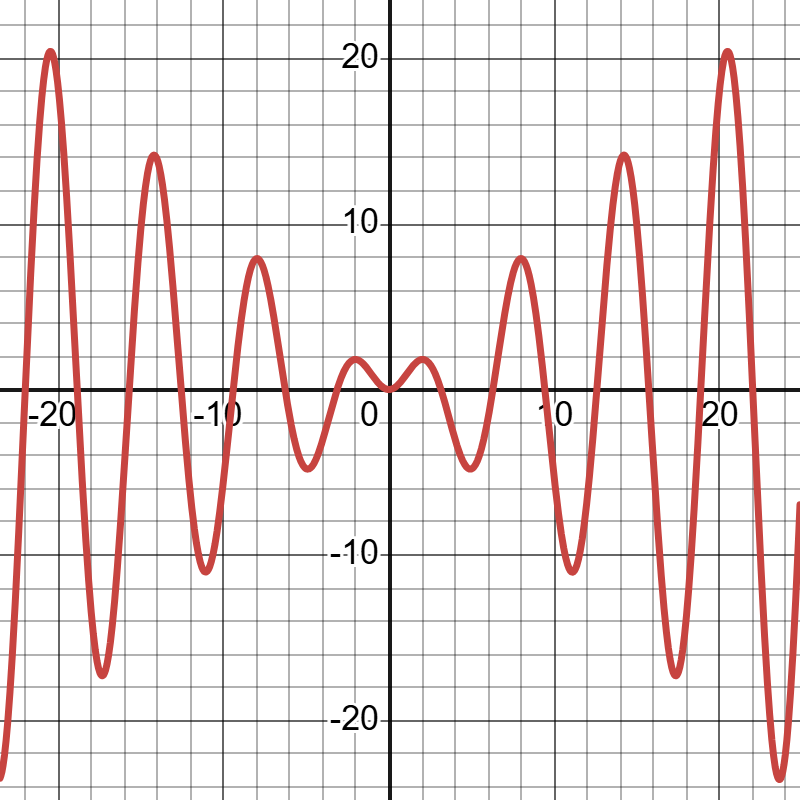
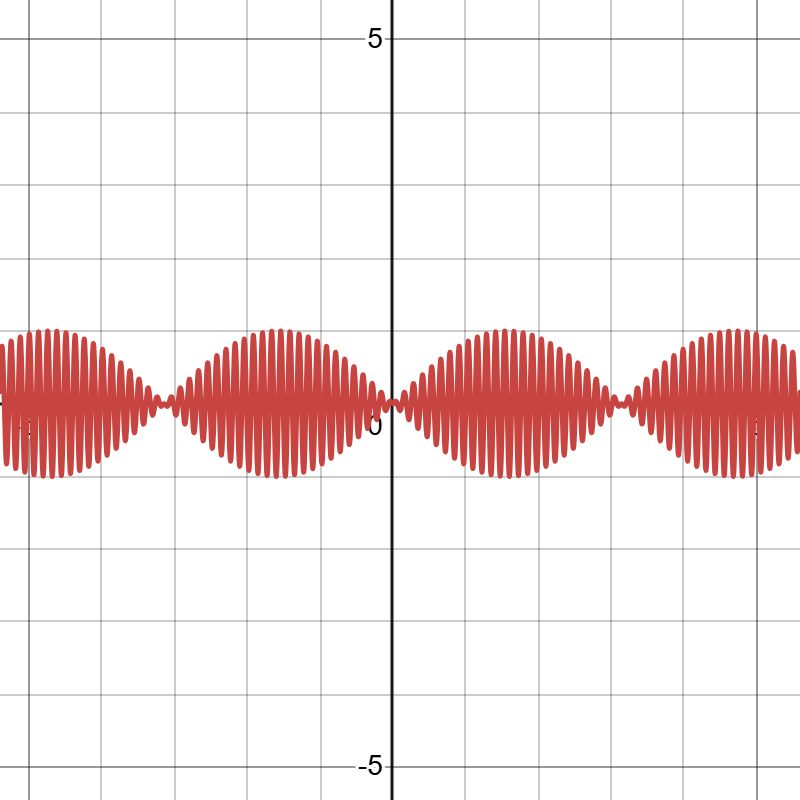
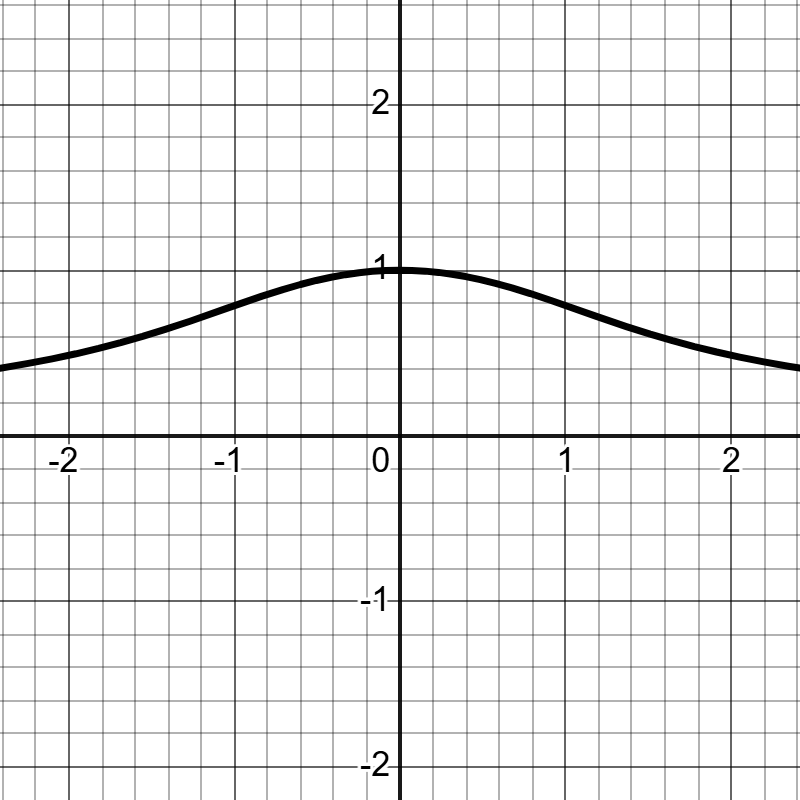
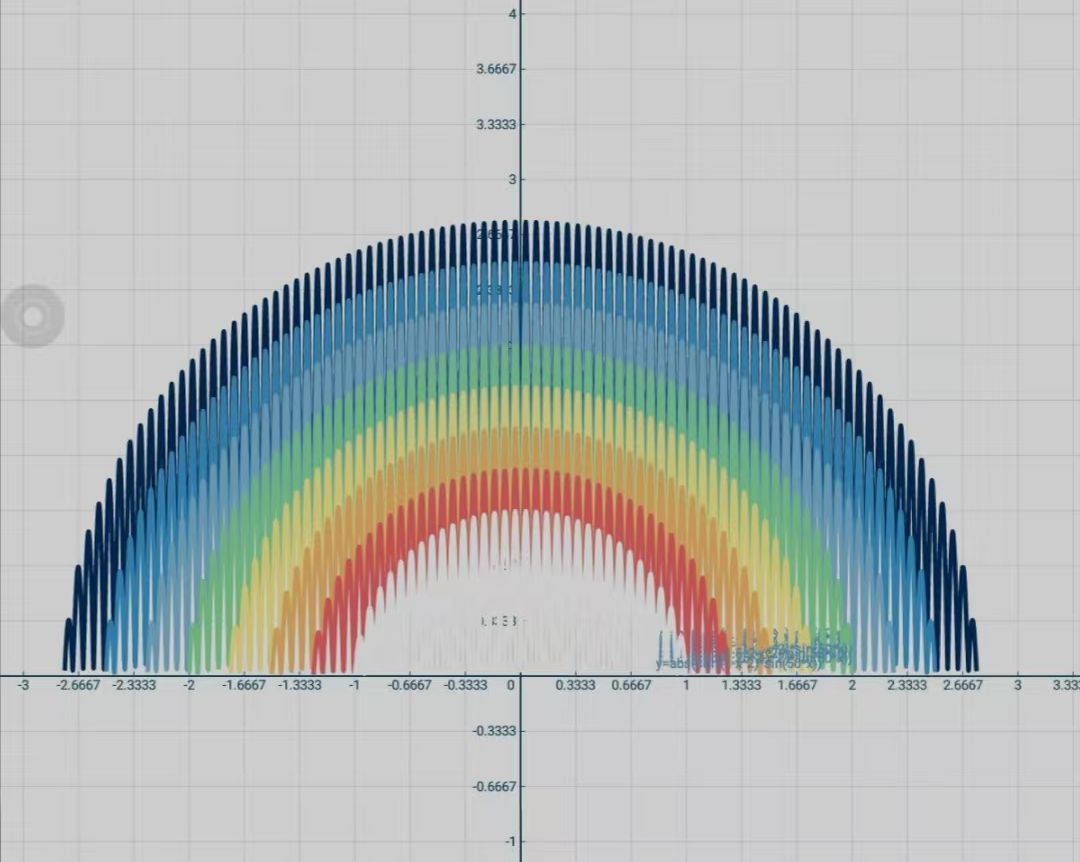
现在有个简单的函数\(h(x)=x\)，我们都知道它的图像是一条直线。那么将它乘上一个\(\sin{x}\)会变成什么呢。我们来试一下。记函数\(f(x)=x\sin{x}\)，其图像如图2。我们发现\(f(x)\)都被夹在\(y=\pm x\)之间。当\(\sin{}\)中的系数增大的时候这一现象会更加明显。那么当\(\sin{}\)里面的系数足够大的时候，我们就可以说\(h(x)=x\)这个函数被填充完成了。

现在我们不妨再看看其它的函数图像。

发现了函数的填充有一个特点，那就是填充是上下对称的，这是因为\(\sin{x}\)的值域为\((-1, 1)\)。要是想要上下不对称填充要怎么办呢？接下来神奇的拉伸变换就能够完成这件事。

二、函数的拉伸变换：\(g(x) + ...\)

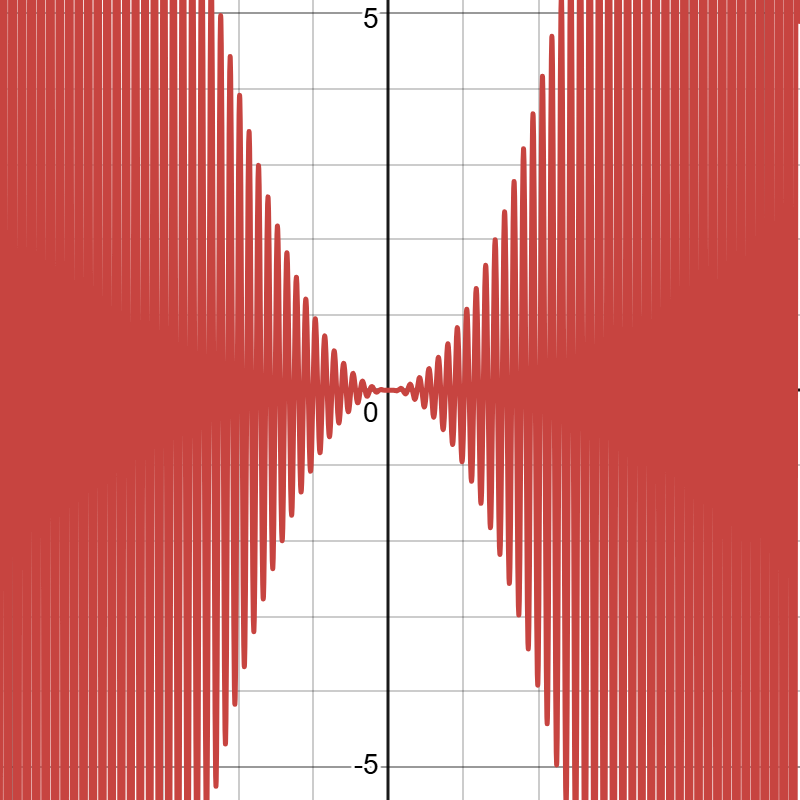
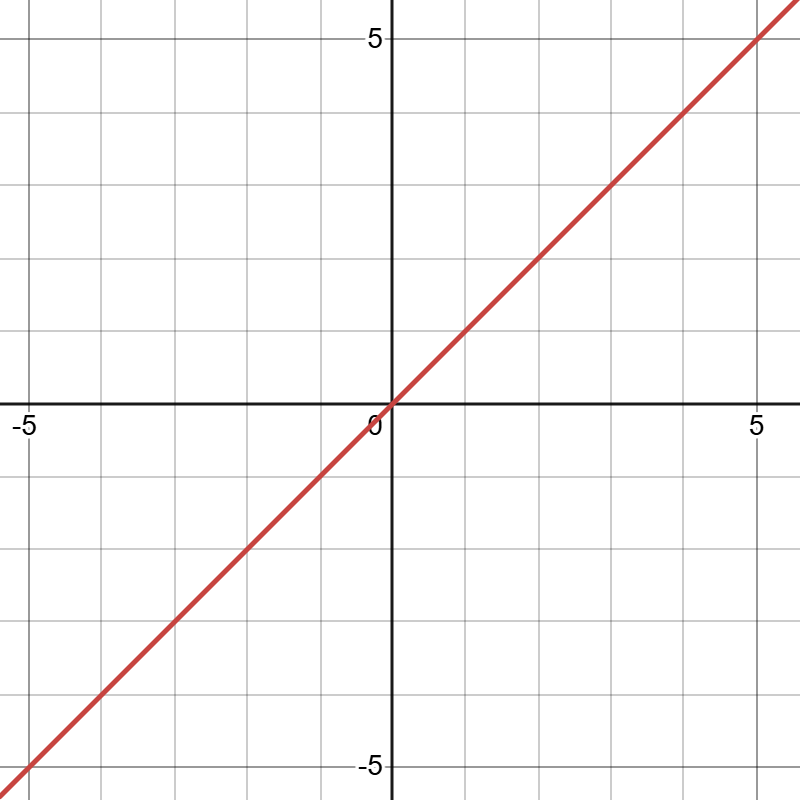
还是有一个最简单的函数\(f_0(x)=x\)，将它加上一个\(\sin{x}\)会发生什么呢？我们记\(g(x)=\sin{x}\)，则\(f_1(x)=g(x)+h(x)=\sin{x}+x\)，其图像的变化如下：

图4: 函数图像变化前

图5: 函数图像变化后

发现了一个神奇的现象：\(f_1(x)\)的函数图像刚好是将\(x\)轴的形状从直线拉伸变换成了\(\sin{x}\)的形状，然后\(h(x)\)在这个新坐标系（\(x\)轴经\(g(x)\)拉伸变换得到的坐标系）中的图像再对应到原坐标系中的图像。当\(g(x)=x\)时候，可能会更好理解，如下图：

图6: 函数图像变化前

图7: 函数图像变化后

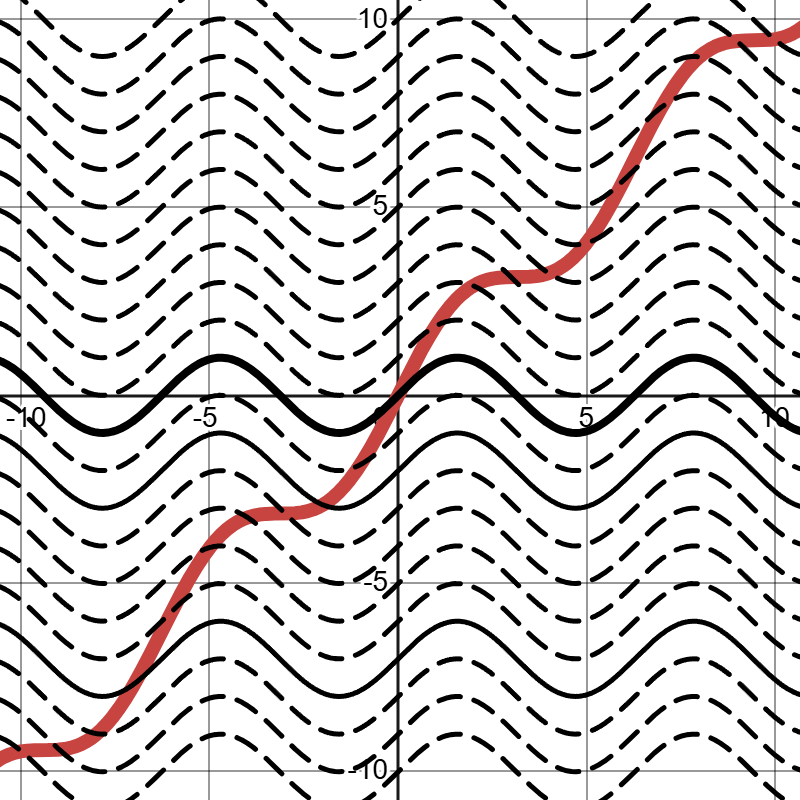
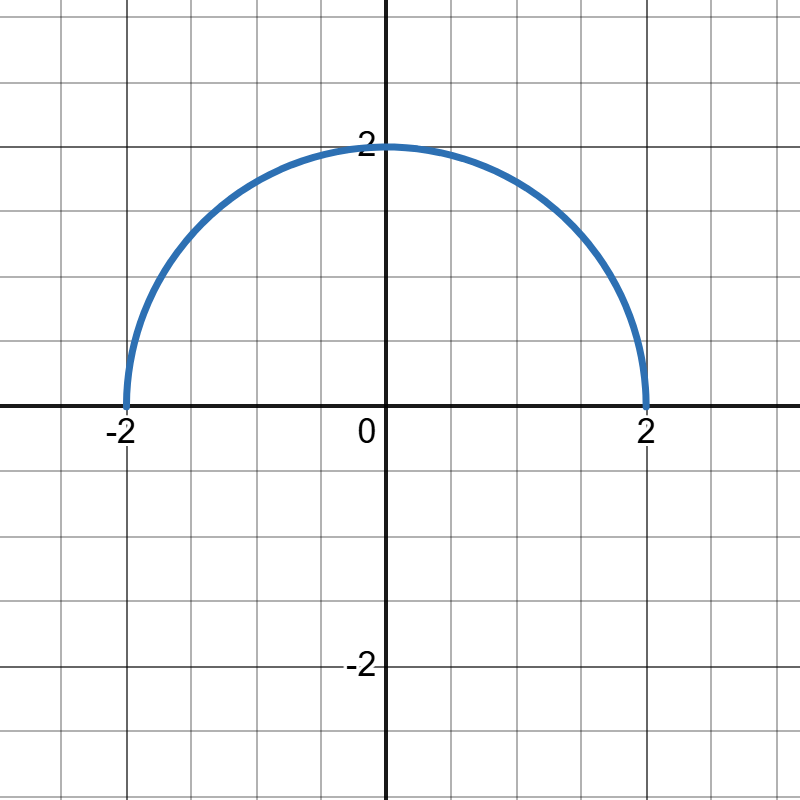
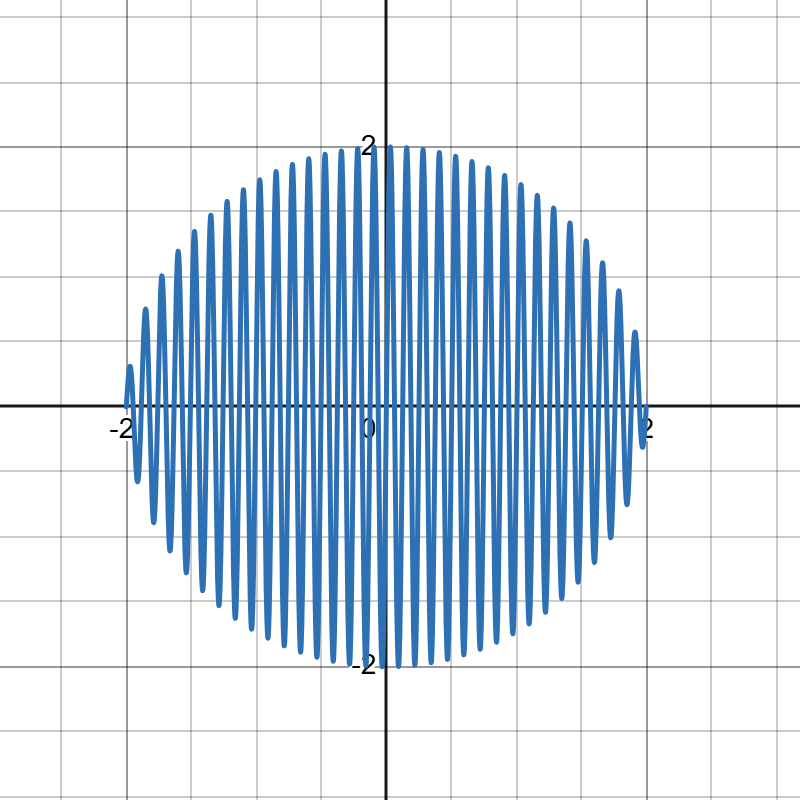
这样一来只需要控制好拉伸变换的函数\(g(x)\)，就可以将原先对称填充的函数变成想要的图案。比如可以将半圆函数 \[f_0(x)=\sqrt{4-x^2}\] 填充为 \[f_1(x)=\sqrt{4-x^2}\sin{50x}\] 再拉伸为 \[f_2(x)=x+\sqrt{4-x^2}\sin{50x}\]

图8: 半圆函数图像变化前

图9: 半圆函数图像变化后

这样一来，开头的爱心函数就可以画出来了，我们来分析一下：

\[f(x) = \lvert x\rvert ^\frac{2}{3} + \sqrt{4-x^2}\sin{50x}\]

现在来拆解一下这个函数：\(g(x)=\lvert x\rvert ^\frac{2}{3}\)是用来拉伸变换的，\(h(x)=\sqrt{4-x^2}\)是用来控制形状的，最后的\(\sin{50x}\)是用来填充的。连起来说就是：爱心函数是以半圆函数\(h(x)=\sqrt{4-x^2}\)为胚用\(\sin{50x}\)填充为一个整圆再用\(g(x)=\lvert x\rvert ^\frac{2}{3}\)拉伸而得到的。绘制的过程如下：图10\(\rightarrow\)图11\(\rightarrow\)图12

图10: 半圆函数

图11: 填充

图12: 拉伸

所以以\(h(x)\)为原型经过填充和拉伸变换后再结合多个函数的组合就可以画出好多好看的函数图像。现在还剩下最后一点没有讲。

三、函数图像定义域的控制：\([(n-x)(x-m)]^\frac{1}{1000}\)

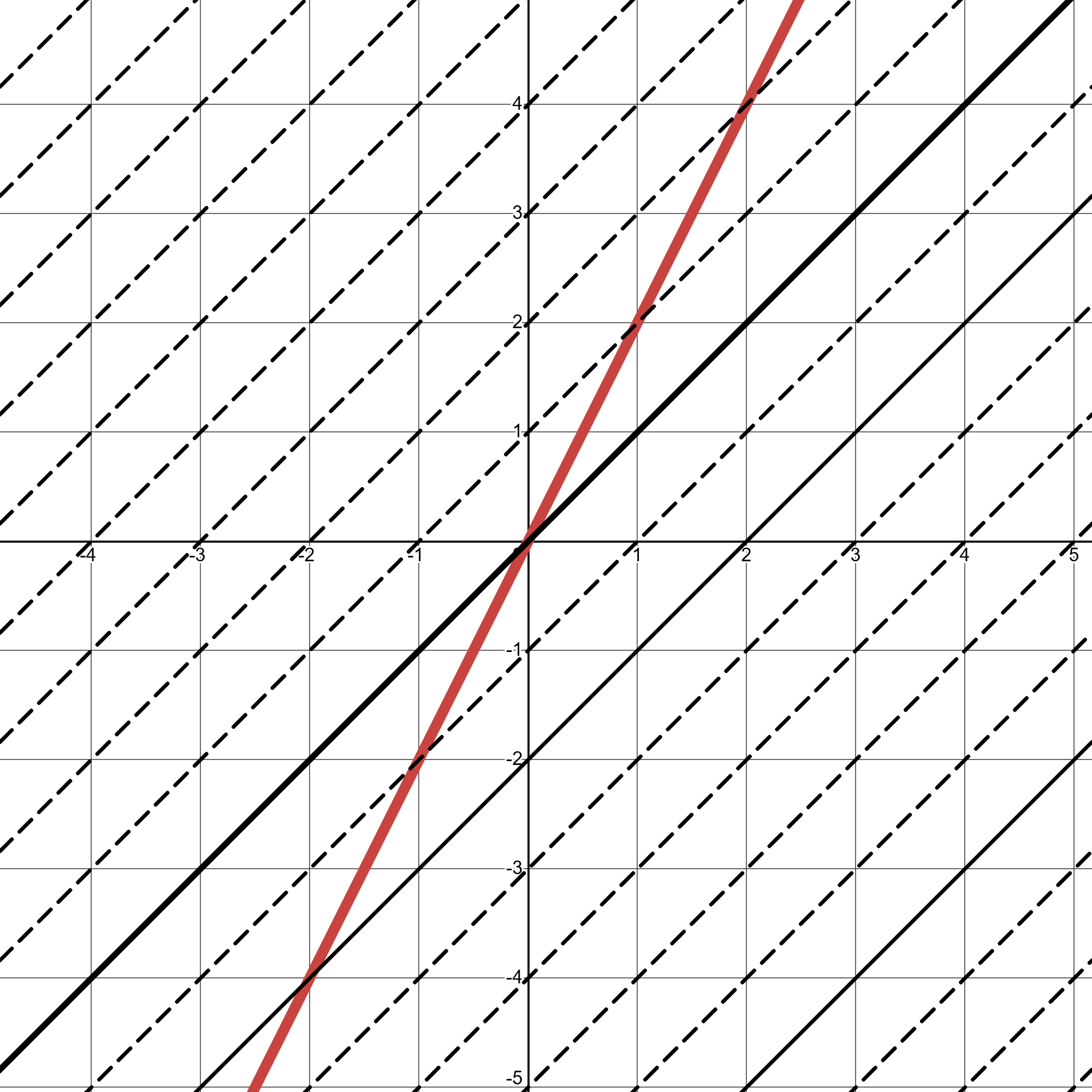
如果说我们不想让函数显示完整的图像，而是只显示指定的一部分图像要怎么办呢？很简单，将函数表达式乘上\([(n-x)(x-m)]^\frac{1}{1000}\)就可以了。这就在几乎不改变原来函数图像的基础上限制它的定义域在\([n,m]\)之间，其中\(n<m\) 。

至于为什么是这样呢？一般来说，一个定义域为\(D_1\)的函数\(f_1\)乘上一个定义域为\(D_2\)的函数\(f_2\)，那么这个新的函数定义域就会变成\(D_1\)和\(D_2\)中较小的那一个。我们知道函数\(f(x)=\sqrt{(n-x)(x-m)}\)的定义域是\([n,m]\)，那么就可以利用这个函数来控制定义域了。不过为什么右上角的次数为\(\frac{1}{1000}\)呢？因为当函数乘以\(\sqrt{(n-x)(x-m)}\)时对原函数图像的变动较大。而除\(0\)以外任何数的\(0\)次方都为1，所以当指数越接近\(0\)时，对原函数图像的变动就越少。

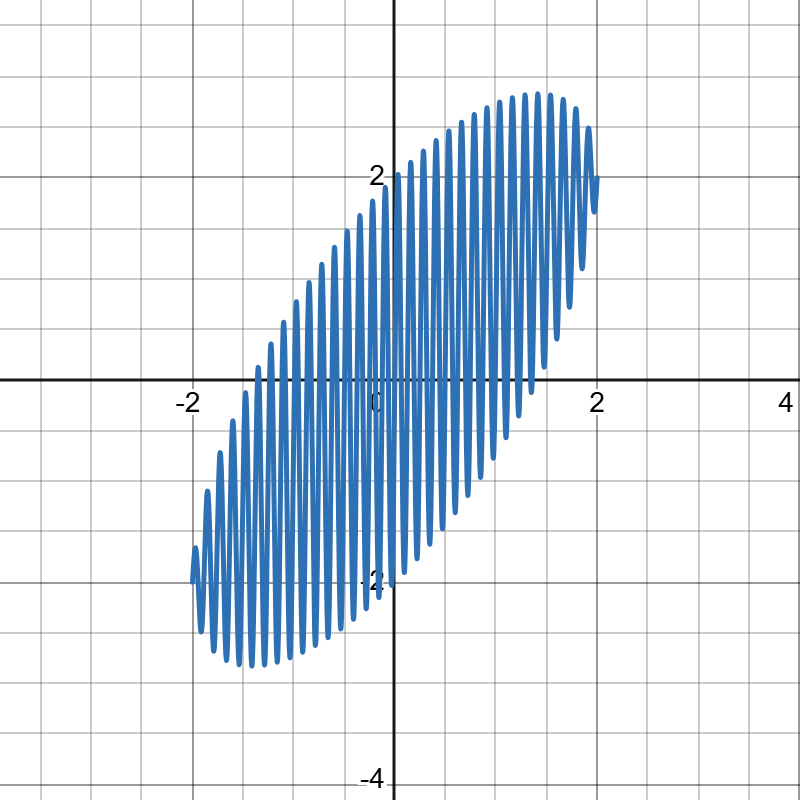
这样的话我们就可以将刚刚画好的爱心分一半给别人啦。

图13: 左边半个爱心
_{控制定义域为[-2, 0]}

图14: 右边半个爱心
_{控制定义域为[0, -2]}

OK啦，现在有关用函数画画的内容基本都说完了，最后再来总结一下： \[f_{draw}(x) = [T_{stretch}(x)+S_{base}(x)\cdot\sin{(D_{f}\cdot x)}]\cdot[(n-x)(x-m)]^\frac{1}{I_{d}}\] \(f_{draw}(x)\)的图像是由基础形状函数\(S_{base}(x)\)在经过正弦填充函数\(\sin{(D_{f}\cdot x)}\)填充后再用变换拉伸函数\(T_{stretch}(x)\)拉伸，最后经过\([(n-x)(x-m)]^\frac{1}{I_{d}}\)的定义域控制得到的。其中，\(D_{f}\)是填充系数，\(D_f\)越大，填充越密，建议值\(50\)；\(I_d\)是定义域影响因子，\(I_d\)越大，对函数图像的变动越小，建议值\(1000\)。

接下来我们一起画一个函数桥来结束本篇。

四、画一个函数桥！

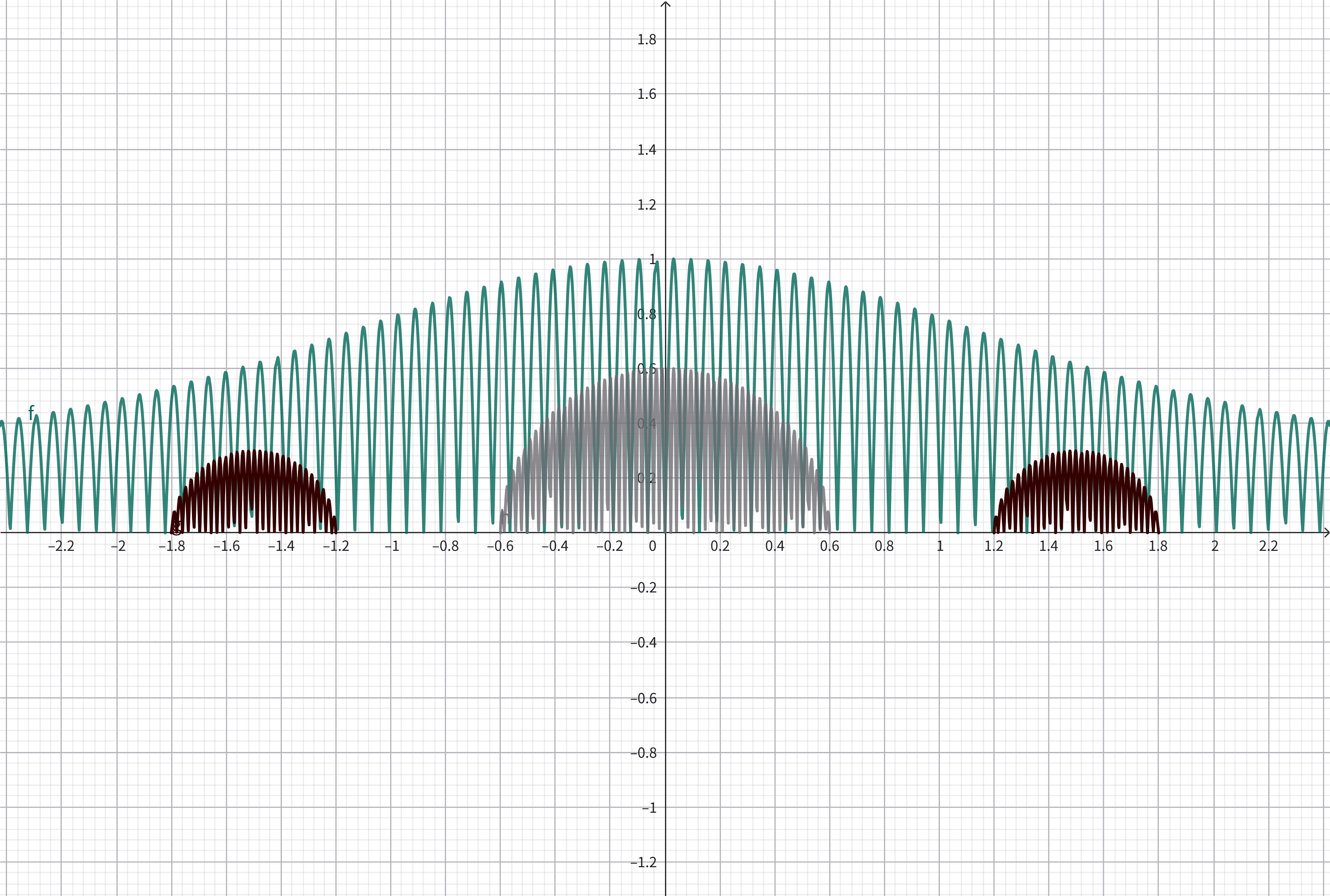
既然要画一个桥，那么我们就需要有个合适的函数作为基础形状函数\(S_{base}(x)\)，这里刚好有一个合适的函数： \[S_{base}(x)=\sqrt{\frac{1}{2}(\sqrt{x^4+4}-x^2)}\] 这个函数应该是来自于我高中时候写的某一道题。它的图像如图15。

图15: 函数桥的基础形状函数

然后再用正弦填充函数\(\sin{(50\cdot x)}\)对它进行填充。由于我们不想要上下对称填充，所以这里我们可以用个小技巧来只填充上半部分——对填充函数取个绝对值。这样我们就得到了：

\[\sqrt{\frac{1}{2}(\sqrt{x^4+4}-x^2)}\cdot\lvert \sin{50x}\rvert\]

它的图像见图16。

图16: 只填充上半部分

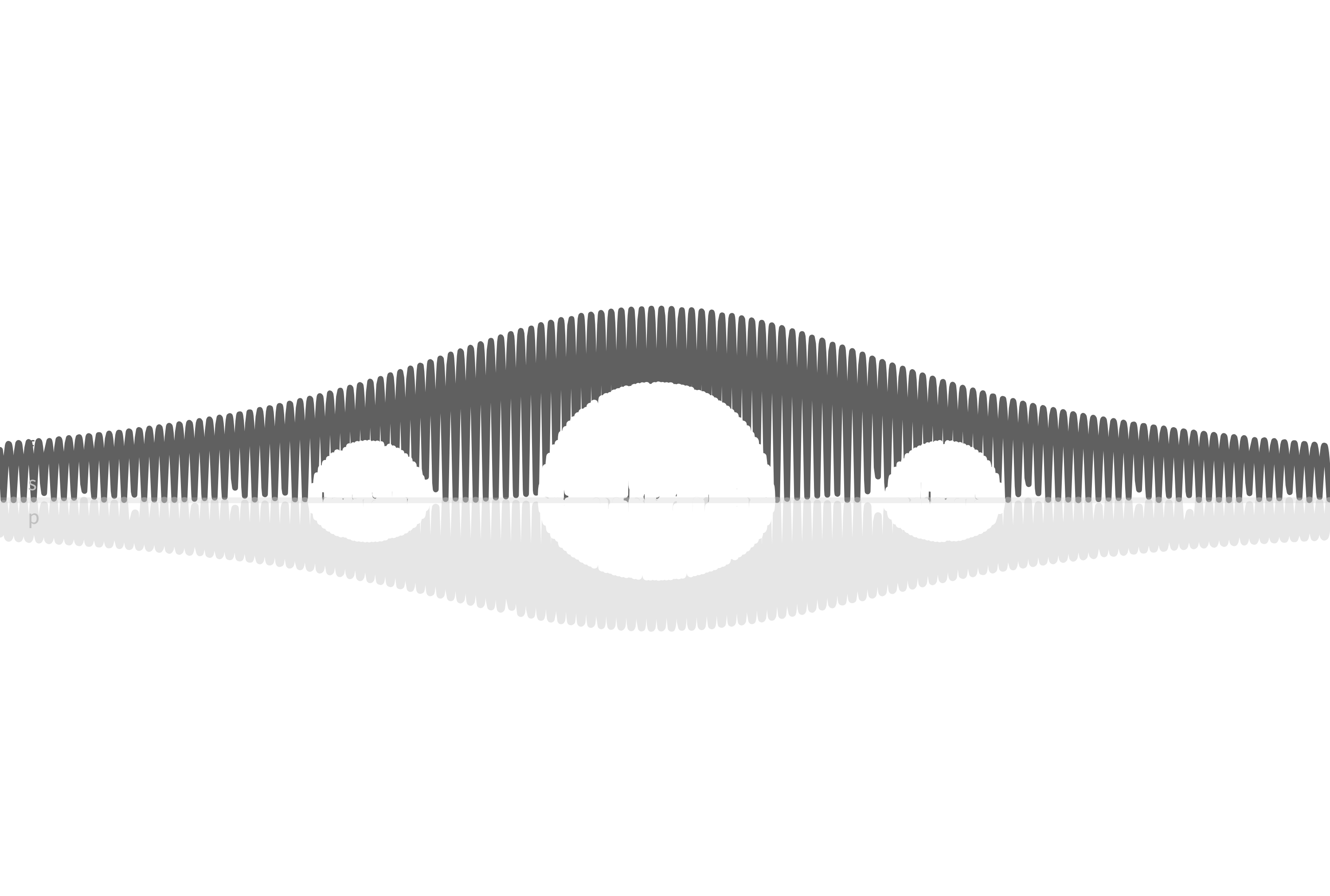
由于它是一座桥，我们还需要对其加上几个桥洞。所以用半圆函数画出函数桥洞。

\[桥洞1：\sqrt{0.3^2-(\lvert x\rvert -1.5)^2}\cdot\lvert \sin{(150\lvert x\rvert)}\rvert\]

\[桥洞2：\sqrt{0.6^2-x^2}\cdot\lvert \sin{150x}\rvert\]

现在的图像如下：

图17: 加上桥洞

最后我们给它加上再水中的倒影，也就是给上面的函数加个负号并改变一下它们的系数和颜色，函数桥就完成啦！

图18: 函数桥

它的表达式为： \[ \begin{cases} f_1(x)=\sqrt{\frac{1}{2}(\sqrt{x^4+4}-x^2)}\cdot\lvert \sin{50x}\rvert & \text{桥体} \\ f_2(x)=\sqrt{0.3^2-(\lvert x\rvert -1.5)^2}\cdot\lvert \sin{(150\lvert x\rvert)}\rvert & \text{桥洞1}\\ f_3(x)=\sqrt{0.6^2-x^2}\cdot\lvert \sin{150x}\rvert & \text{桥洞2}\\ f_4(x)=-\frac{2}{3}f_1(x) & \text{桥体倒影}\\ f_5(x)=-\frac{2}{3}f_2(x) & \text{桥洞1倒影}\\ f_6(x)=-\frac{2}{3}f_3(x) & \text{桥洞2倒影} \end{cases} \]