通过互补滤波获取姿态角度

  最近在做轮腿小车，其中需要通过陀螺仪获取小车的实时角度值。学习了一下有关互补滤波的内容，在此记录一下。

  互补滤波的核心是融合陀螺仪和加速度计的数据，用陀螺仪保证动态响应，用加速度计修正长期漂移，输出稳定且实时的角度估计。

  陀螺仪检测系统的三轴角速度值，加速度计检测三轴的加速度值（在静止状态下，主要检测重力加速度的三轴分量）。根据以上传感器数据，我们需要得到系统的实时姿态角度有两种办法：1. 通过陀螺仪给出的角速度数据积分得到角度值；2. 通过加速度计给出的加速度数据进行反正切运算得到角度值。

1. 角速度积分得到角度值

方法

  我们知道，在极小的一段时间\(\Delta t\)内可以将系统的运动视为匀速。因此这段时间内转过的角度为\(\Delta \theta = \omega \Delta t\)。对其进行积分就可以很容易得到当前的角度值：

\[\theta_{gyro} = \int_0^t\omega dt\]

局限性

  但是这种方法存在一个问题，就是从陀螺仪获取的角速度数据每时每刻都存在误差，而积分这种操作会将这种误差累积导致积分得到的角度值存在漂移。而这种漂移误差在低频段会被积分放大，最终主导输出结果，使得角度严重偏离真实值。而在高频场景下，例如小车快速晃动，此时陀螺仪的有效角速度信号远大于低频漂移的信号，此时对最终角度的影响可以忽略。

  所以总结一下，通过角速度积分得到的角度值在动态情况下表现尚可，而在静态情况下表现欠佳。

2. 加速度数据反正切得到角度值

方法

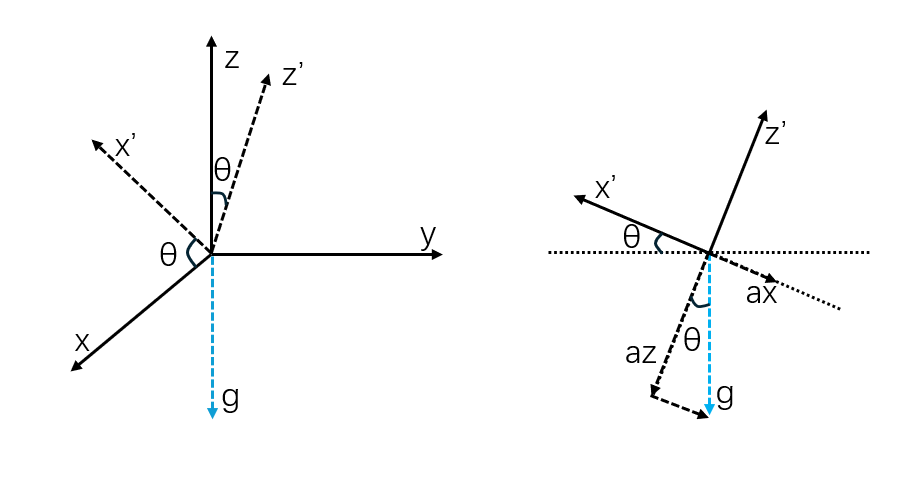
  假定在静止状态下让系统绕y轴旋转一个角度\(\theta\)，根据以上分析可以很容易得出系统的俯仰角：

\[\theta_{acc} = \arctan \frac{ax}{az}\]

局限性

  但是这种方法同样也存在一个问题，就是高频段的振动干扰和运动加速度会掩盖有用的重力信号，无法准确获取静态角度参考。比如快速晃动小车，加速度计的输出是重力加速度、高频运动加速度的叠加，此时有用的重力信号被高频干扰淹没，无法通过加速度计计算出准确的角度。

  总结一下，就是通过加速度反正切得到角度值在静态情况下表现尚可，而在动态情况下表现欠佳。

3. 通过互补滤波修正角度值

  通过以上分析，我们可以发现陀螺仪和加速度计的频率特性是互补的。因此我们可以对其取长补短，在动态条件下更相信陀螺仪的数据，在静态条件下更相信加速度计的数据。

原理

  通过设定权重参数\(K\)来选择我们是更相信陀螺仪的数据还是更相信加速度计的数据，所以最后的角度输出为：

\[\theta_{out} = K * \theta_{gyro} + (1-K) * \theta_{acc}\]

  权重参数\(K\)的具体选择需要根据系统的具体应用场景来分析。

实现

具体实现代码如下：

/*
  一阶互补滤波，标准版本
  gyro_    陀螺仪物理数据    °/s
  acc_     加速度计物理数据  m/s^2
  filter_value->filtering_angle 存放滤波后的角度数据，为真实物理量，单位为角度制
*/
void FOCF_v2(float gyro_, float acc_, FOCF_STRUCT *filter_value)
{
    float angle_gyro;    // 由陀螺仪计算得到的角度
    float angle_acc_rad; // 由加速度计计算得到的角度（弧度制）
    float angle_acc;     // 由加速度计计算得到的角度（角度制）
    
    angle_gyro = filter_value->angle_temp + gyro_ * filter_value->call_cycle;    // 积分得到陀螺仪角度
    filter_value->angle_temp = angle_gyro;
    
    angle_acc_rad = atanf(acc_ / acc_z_);
    angle_acc = to_deg(angle_acc_rad);      // 反正切得到加速度计角度并转化为角度制
    
    // 加权求平均并修正零点
    filter_value->filtering_angle = filter_value->v2_K * angle_gyro + (1 - filter_value->v2_K) * angle_acc + filter_value->mechanical_zero;
}